3 à Numerador
-----
4 à Denominador
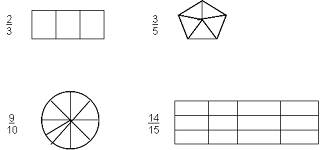
1. Coloreo en cada figura la fracción del area,
que se indica.
1. Escribo
en forma de fracciones
- Quince tercios
- Veintinueve cuartos
- Ciento dos sextos
- Doce milésimos
- Tres doceavos
Con las fracciones
representamos la relación entre el todo y sus partes.
2. COMPLETO
LA TABLA
REPRESENTACIÓN GRÁFICA
|
NUMERO DE PARTES EN QUE SE DIVIDIO LA UNIDAD
|
NUMERO DE PARTES SOMBREADOS
|
NUMERO DE PARTES DE no SOMBREADOS
|
FRACCIÓN REGIÓN
|
SOMBRA
|
NO SOMBRA
|
|
|
3
|
1
|
2
|
1
3
|
2
3
|
|
|
|
|
|
|
|
|
6
|
|
|
5
6
|
|
|
|
|
|
|
|
|
|
|
|
8
18
|
|
Para
calcular la fracción de un numero hay dos formas del hacerlo.
Dividimos,
el número entre el denominador de la fracción y el resultado, lo multiplicamos
por el numerador.
Otra forma
es multiplicar el número por el numerador y se divide por el denominador.
1
--- de 54 à 54 ÷ 6 = 9 y 9 * 1 = 9
6
1
--- de 54
= 9
6
4. En una finca e mi vereda hay 84 animales. 1/4
del total son vacas: 2/7 son cerdos; 1/3 son aves y el resto son diversos
animales. Pido explicación a mi profesor (a)
para resolver la situación.
5. Resuelvo las operaciones y completo el gusano
FRACCIONES EN LA
RECTA NUMERICA
Las
fracciones se pueden representar en rectas numéricas. Para
representarlas basta dividir cada segmento que se toma como unidad en tantas
partes iguales como indica el denominador y desplazarse o tener en
cuenta las partes que indica el numerador.
Ejemplo:
6. Escribe la fracción que indica cada letra
7. Una hormiga realiza el siguiente
desplazamiento en dirección hacia su hormiguero. Recogió una hoja y recorrió
3/7 del camino. Tropiezo con una piedra y perdió la hoja. Luego recorrió 1/7
del camino sin llevar nada. Recogió una semilla y recorrio 2/7 del camino con
ella.
* Representa
en la recta numérica los desplazamientos
de la hormiguita (uno detrás del otro). Toma el punto cero como el lugar de
salida y el 1 como el hormiguero.
¿Qué
fracción del camino le falta para recorrer el hormiguero?
FRACCIONES EQUIVALENTES
Dos o más
fracciones son EQUIVALENTES
cuando representan la misma parte de un todo o de una cantidad.
Dos
fracciones son equivalentes si al multiplicar el numerador de una con el
denominador de la otra, los productos obtenidos son iguales.
3
6 3 * 10 = 5 * 6
3 6
--- ----
=
----- = ------
5
10 30 = 30 5 10
1. Encierro
las parejas de fracciones equivalentes
7
14
6 3
a. ----
y ----- d. ------
y -------
5 10 12 6
3 12 1 4
b. ----
y ----- e. ------
y -------
4 16 3 12
5
10
4 6
c. ---- y
-----
f. ----- y
------
2 4 7 28
9. Colorea las fracciones equivalentes, teniendo
en cuenta, el código de colores.
1 2 3 4
Azul ----- Rojo ---- Verde -----
Amarillo ----
2 3 5 7
10. En cada grupo marco con X la fracción que no
es equivalente con las demás y justifico
2 4 6
12 20
---- à ---- , ----,
----, ----
3 6 4
18 30
16 8 2
24 48
---- à -----, -----, -----, ----
18 9
3 27 54
4 2 8
3 12
--- à ----,
----, ----, -----
10 5
20 15 30
Para escribir una Fracción Equivalente a otra con
números mayores, multiplicamos el numerador y el denominador de la fracción por
el mismo número. Este proceso se llama complificacion.
Ejemplo:
2
Complicamos 7 por la
fracción ----
3
11. Compliquemos las fracciones por 3
2
4 5 6
--- ----- ---- ----
3
7 3 5
12. Completo los diagramas escribiendo el
operador empleados en cada complicación.
7 21 12 24
a ----- *
---- = -----
b. ------ * ----- = -----
8 24 5 10
7 21 21 42
c ----- *
---- = -----
b. ------ * ----- = -----
3 9 5 10
Para
escribir una fracción equivalente a otra con números menores, dividimos el
numerador y el denominador de la fracción por el mismo numero. Esto proceso se
llama SIMPLIFICACIÓN.
Ejemplo:
24
Simplifiquemos
la fracción -----
36
24 12 2
---- ÷ ------
= ----
36 12 3
13. Completa cada diagrama escribiendo el
operador empleado en cada simplificación.
24
8
a. -----
= ----- Operador empleado 3
15
5
72
8
b.----- =
---- ________________________
27
3
48
6
c. ----- =
---- __________________________
40
5
63
9
d. ---- =
---- __________________________
28
4
14. Simplifica cada fracción
20 12 32
a.
----- = ____ b.
----- = _____ c. ------ =
______
15 24 28
42 81 25
d.
----- = ____ e.
----- = _____ f. ------ =
______
49 18 35
UN CAMINO QUE
PERMITE AL SAPO LLEGAR AL LUGAR DONDE SE ENCUENTRA EL GUSANO TIENE TODAS LAS
FRACCIONES EQUIVALENTES. ENCUENTRALO Y COLOREA LAS PIEDRAS CORRESPONDIENTES.
ejercicios: Si dos fracciones tiene igual denominador, es mayor la fracción que tiene mayor el numerador.
Si dos fracciones tienen diferente denominador, se
buscan fracciones equivalentes a las dadas que tengan el mismo denominador y se
comparan las fracciones equivalentes.
Ejemplo:
Comparemos
las fracciones:
5
3
--- ---
7
7
Tiene igual
denominador, comparamos los numeradores 5 > 3 entonces….
5
1
--- >
---
7
3
Si tienen
diferente denominador
2
1
--- y
----
5
3
2
2 * 3 6 1 1 * 5 5
--- = --------
= ---- ---- =
-------- = ----
5
5 * 3 15 3 3 * 5 15
6
5 2 1
--- >
---- luego ----
> -----
15 15 5 3
1 ESCRIBO > O < , SEGÚN CORRESPONDA.
a. 2
3 b. 8
3 c. 3
9
---- ---- ---- ----- ----- ----
4 4 10 10 7 7
4
11
9 19 13 11
d. ---
---- e.
---- ----- f. -----
-----
9 9 3 3 5 5
Las fracciones que
representamos con un número entero y una fracción propia se llaman números mixtos.
17
* Transformemos la fracción ----- en número mixto
6
- Realizamos
la división del numerador entre el denominador.
5
- Escribimos el numero mixto: 2 ---, en donde 2 es el cociente.
6
5 el residuo y 6 el divisor.
2. EXPRESA COMO NUMERO MIXTO CADA UNA DE LAS
SIGUIENTES FRACCIONES Y AL FINAL ORDENALAS DE MAYOR A MENOR.
6 3 25
a. ---- = b. ----- = c. ------ =
5 2 9
9 15 18
d. --- = e. ------ = f. ----- =
3 4 3
3. RELACIONA CADA NÚMERO MIXTO CON SU FRACCION
CORRESPONDIENTE.
2
49 3 ---
---- 7
9
3 18
5 --- -----
8 5
4
23 5 ---
--- 9
7
3 43
3 --- ----
5 8
3. COMPLETO
CADA EXPRESIÓN:
4
a. 3
---- = ------
5 5
19
b.
------ = ------
3 3
2
c. 5
----- = ------
7
43
d. ------ = ------
10 10
ADICCIÓN Y SUSTRACCIÓN DE FRACCIONARIOS HOMOGÉNEOS
Las fracciones homogéneas
tienen igual denominador.
Para adicionar o sustraer
fracciones homogéneas, se adicionan o sustraen los numeradores y se escribe el mismo denominador, teniendo
en cuenta que el minuendo debe ser mayor que el sustraendo.
No olvide simplificar al
máximo una fracción, siempre que sea posible.
4. REALIZA
LAS SIGUIENTES ADICIONES Y SUSTRACCIONES, SIMPLIFICA SI SE PUEDE.
4 6 10
2 5 23 7
16
---- +
---- = ----- ÷ ----- = ---- ----- - -----
= -----
8 8 8 2
4 25
25 25
12 11 16 34
---- -
----- = ----- +
-----
21 21 17 17
7 13 11 7
--- +
---- = ---- -
----
9 9
5 15
14 5 10 14
---- -
---- = ---- +
-----
18 18 23
23
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES HETEROGÉNEAS
Para
realizar la adición y sustracción con diferente denominador es necesario
volverlas equivalentes. Se adicionan o sustraen los numeradores y se deja el
mismo denominador.
Ejemplo:
Juliana
gastó 1/5 de sus ahorros en la compra de un pantalón y 2/7 en una maleta para
el colegio. ¿Qué parte de los ahorros gasto juliana?
Para saber
que parte de los ahorros gastó Juliana debemos adicionar las fracciones que
indican la cantidad.
Como tienen
diferente denominador debemos buscar fracciones equivalentes que tengan
denominador común al mínimo común múltiplo de los denominadores.
·
Buscamos el m.c.m. de 5 y 7 = 35
1 7 7 2 5
10
--- *
--- = ----- ----- * ------ = ------
5 7 35 7 5
35
Adicionamos:
7 10
17
--- +
----- =
------
35 35
35
17
Juliana
gastó de sus ahorros -----
35
·
Desarrollamos la siguiente sustracción de
fracciones:
11 4
---- - ----
7
3
·
Buscamos el m.c.m. de 7 y 3 = 21
11 3 33 4 7
28
---- - -----
= ------ ----- - ---- = ----
7 3 21 3 7
21
33 28 5
---- -
----- = -----
21 21 21
11 4 5
--- -
---- = -----
7 3 21
5. RESUELVO
LOS SIGUIENTES EJERCICIOS
5 3 5 7
--- +
---- = --- + ---
=
8 2 3 5
6 4 10 7
--- -
---- = ---- - ----
=
3 5 3 8
7 3 7 9
--- +
--- = --- -
---- =
9 4 5 8
6. ENCIERRA
LA RESPUESTA
CORRECTA
8 2 6 11 9 8
--- - ----
= ---- ,
------- , ----- , -----
3 9 72 72 70 72
14 14 15 70 15 16
---- -
----- = ----- , ------ , ------ , ------
5 10
12 50 10 10
4 2 22 45 18 5
--- +
----- = -------, -------, ------- , ------
5 3 15 15 25 15
8. RESUELVO LAS SIGUIENTES SITUACIÓN.
2 31
a. Qué numero debe sumarse a ----
para obtener ----- ------------
7 35
b. Marlon Julián recorre en su bicicleta 9/5 de
kilómetro. Si ya ha recorrido 6/7 de km, Qué parte le falta recorrer?
c. Cuál es la característica principal de una
fracción heterogénea?
LEO, ANALIZO
Y COPIO EL SIGUIENTE EJERCICIO
* Calculemos
el producto de 7/3 y 4/9
7 4 7 * 4 28
--- *
----- = ---------- = ------
3 9 3 * 9 27
5 6 5 * 6 30
--- * ----
= ---------- =
------
8 8 8 * 8 64
Simplifico
: 30 30 ÷ 2 15
--- = ---------- =
----
64 64 ÷ 2 32
a. Qué operación se desarrollo en los anteriores
ejercicios?
b. Qué clase de fracciones son de acuerdo a sus
denominadores?
c. Describo el proceso que se realizo para
obtener el resultado en los ejercicios.
i
9. EFECTUAR CADA OPERACIÓN Y SIMPLIFICA EL
RESULTADO SI ES POSBILE.
3
2 3 9 8 6
a. ---- *
----- = b. -----
* ----- c.
----- * ----
4
5 5 7 9 5
4
7
7 3 1 6 2
10
d ---- *
----- = e. ---- * --- * ---- =
f. --- * ---- = ----
9
2
2 14 3 4 5
3
COPIO
Para multiplicar fracciones
se multiplica los numeradores entre si y los denominadores entre si, así tengan
igual o distinto denominador.
REFUERZO
1. DESARROLLO 2 EJEMPLOS PARA CADA TEMA
·
Términos de la fracción
·
La fracción como parte de un todo
·
Fracciones equivalentes
·
Simplificación
·
Complificación
·
Comparación de fracciones (> o <)
·
Ubicación en la recta numérica
·
números mixtos
·
adición y sustracción de fracciones homogéneas
·
adición y sustracción de fracciones heterogéneas
·
Multiplicación de fracciones
2. RESUELVO LAS SIGUIENTES SITUACIONES
·
Marina gasto 2/5 de la mitad de $10.000 en un helado
de crema. Cuánto costó el helado?
·
Laura tenía ¾ de un cartón de huevos y se le
rompieron 1/3 de los huevos. Qué huevos le quedaron?
·
Libardo tiene 72 mandarinas para vender a sus
compañeros de cuarto grado. Vendió 2/3, empleo 1/6 para preparar jugo y regalo
1/12. cuántas mandarinas le quedaron?